GEOMETRÍA: pruyecciones ortogonales, traslaciones, rotaciones y simetria axial

Geometría

La geometría es una parte de la matemática que se encarga de estudiar las propiedades y las medidas de una figura en un plano o en un espacio.

• La geometría apela a los denominados sistemas formales o axiomáticos (compuestos por símbolos que se unen respetando reglas y que forman cadenas, las cuales también pueden vincularse entre sí) y a nociones como rectas, curvas y puntos entre otros.

Proyecciones Ortogonales 

La proyección ortogonal es aquella cuyas rectas proyectantes auxiliares son perpendiculares al plano de proyección (o a la recta de proyección), estableciéndose una relación entre todos los puntos del elemento proyectante con los proyectados.

• Proyección ortogonal de un punto sobre una recta

La sombra producida por una figura depende de la posición del foco luminoso que inside sobre ella. La sombra que forma un objeto en el mediodía es una proyección ortagonal del objeto sobre el suelo, porque los rayos del sol inciden perpendicularmente.

Proyección ortogonal de un segmento 

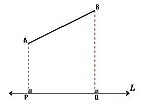
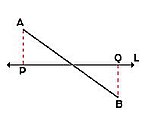
1. Caso general: si el segmento dado AB no es paralelo a la recta L, la proyección ortogonal es un segmento PQ que se obtiene trazando líneas perpendiculares a L desde los puntos extremos de AB. La magnitud de la proyección siempre es menor que la del segmento dado.

2.Si el segmento PQ y la recta L son paralelos, la proyección será: AB = PQ, que se obtiene de forma análoga.

3. Si el segmento AB tiene un punto común con la recta L, la proyección se obtiene de modo similar.

4.Si el segmento AB corta a la recta L, la proyección se obtiene de forma análoga.

• Casos particulares de proyección ortogonal

•  Proyección de un punto sobre una recta. Sea P un punto y m una recta se tiene que: 

  

• Proyección de un segmento sobre una recta. Proyectar un segmento sobre una recta dependerá de la posición del segmento con respecto a la recta.

Translaciones

Las traslaciones pueden entenderse como movimientos directos sin cambios de orientación, es decir, mantienen la forma y el tamaño de las figuras u objetos trasladados, a las cuales deslizan según el vector.

• Transformaciones en el plano: Cuando una persona se desplaza desde una posición a otra , se dice que hizo una transformación del espacio. Si se translada un punto o una figura, se experimenta una transformación en el plano.
• Translación: Se puede allar un punto cualquiera a través de una translación segun un vector dado. para ello se traza un vector equipolente al dado, cuyo origen sea el punto.

EJEMPLO: Determina la imagen del punto P a través de una translacion por el vector u.

Translaciones en el plano carteciano:

para allar la imagen de un punto M dado un vector de translación u, se traza un vector equipolente al vector u partiendo de M. El punto extremo del vector trazado es la imagen de M según T u, es decir, M´. Por ejemplo en el gráfico de abajo, la imagen del punto M (3,1) según el vector u es el punto M(4,2).

Cálculo de las coordenadas de la imagen de un punto según una translación:

para obtener las coordenadas de un punto, que es imagen de otro dado mediante un vector de trasladación, se usa la propiedad que indica que los componentes de dos vectores equipolentes son iguales. 

A CONTINUACIÓN  se muestra el punto P´( x´, y´) como imagen de p(x, y) a través de T u  donde u= (h, k) (con x´, y´, x, y, h y k positivos) :

Traslación de un segmento:

La imagen de un segmento, mediante un vector de traslación, se determina hallando las imágenes de los extremos del segmento a través del mismo vector y trazando el segmento que une las imágenes. Por ejemplo, la traslación aplicada el segmento AB,  a través de u es:

Traslación de una recta:

Al igual que con los segmentos, la traslación de una recta es otra recta paralela a ella.

 Traslación de un ángulo:

  Para determinarla se hallan las imágenes del vértice y luego las imágenes de las semirectas que conforman el ángulo.

(B) BAJO UN VECTOR DE TRASLACIÓN u

 Traslación de un polígono:

Traslación de una circunferencia

Composición de traslaciones: 

Rotaciones

Es el movimiento de cambio de orientación de un cuerpo o un sistema de referencia de forma que una línea (llamada eje de rotación) o un punto permanece fijo.

Movimientos rotatorios:

• Algunos elementos de la naturalezaa o algunos objetos, describen movimientos de rotación, bien sea en sí mismos o con respecto a otro.

OTROS TIPOS DE ROTACIONES:

Determinación del centro de rotación:

 Conocer el centro de rotación de un objeto, resulta conveniente para calcular el movimiento que realizará el mismo. Por ejemplo, para que la rueda de un carro funcione a la perfección, el ejede la rueda debe ubicarse justo en el centro de rotación, de lo contrario, la rueda perdería estabilidad.

 De igual manera, si se quiere determinar el centro de rotacion de un segmento o polígono, se trazan segmentos que unan dos extremos o vértices y con las mediatrices de esos segmentos se encuentra el centro de la rotación.

Simetria axial

Es una transformación del plano o del espacio en la cual, a cada punto P se asocia oto punto P´ llamado (imágen de P), de manera que P y P´ están a igual distancia de una recta llamada (eje de simetria), y el segmento PP es perpendicular a dicho eje. 

  Imagen simétrica de un segmento:

     La imagen simétrica de un segmento, dado un eje de simetría, se determina hallando la imagen de cada extremo del segmento, luego se traza el segmento que une ambas imágenes.

Imagen simétrica de un polígono y de una circunferencia respecto a un eje de simetria:

   La imagen simétrica de un polígono respecto a un eje de simetría se parece mucho a la imagen de un objeto reflejado en un espejo. Para determinarla se halla la imagen simétrica de cada uno de los vértices del polígono, de la misma forma como se determinó la imagen simétrica de un segmento. LUEGO SE UNEN.

GRACIAS POR VER MI BLOG...COMENTA !!!